2016年 東京医科歯科大学 問題分析・解答への道筋

全体の所感

2016年は，力学（惑星運動）と電磁気学（直流回路，ダイオード）からの出題でした。例年通り，前半部分は基本事項を問われており，後半は計算力と思考力を問われる問題が出題されています。今年度の医学科問題（力学の問9，10，電磁気学の問8，問9）は，知識を要する問題も含まれており，例年より難易度の高い出題であると感じられました。また，惑星運動の問題は2年連続での出題でしたが，昨年度の惑星運動の問題に比べて共通問題も難易度の上昇が見られました。

医学部受験生にとっては問題数が多く，時間内に全ての問題を完答するのは厳しかったように感じられます。特に2016年は上でも述べたとおり，医学部問題の難易度が高かったため，これらの問題が解けなくても大きな差は付かなかったでしょう。共通問題をいかに正確に解き切れるかが大切です。

第1問―惑星運動

2015年に引き続き，惑星運動からの出題でした。昨年度に比べて全体的に難易度が上昇しています。楕円の長半径，短半径，面積に関する知識や，エネルギーと軌道の関係の知識があれば見通しが良くなる問題が複数見られました。

問1，問2は円軌道を描く惑星運動の問題です。昨年度も同様の出題がなされているため，全ての受験生がスムーズに解けた内容だと思われます。

問3から問6にかけては，楕円軌道を描く惑星の基本問題です。近日点と遠日点において，エネルギー保存則と面積速度保存則を連立する，という流れと計算手順が身についていれば，時間をかけることなく解ける内容となっています。

問7は楕円の数学的な問題です。太陽と近日点の距離を$r_1$，太陽と遠日点の距離を$r_2$とすると，楕円の長半径$a$および短半径$b$は， $$a=\frac{r_1+r_2}{2},\ b=\sqrt{r_1r_2}$$ で与えらることは記憶しておくべきでしょう。楕円の面積$S$が，$a,\ b$を用いて， $$S=ab\pi$$ で与えられることも必ず記憶しておくべきです。これらの公式さえ覚えていれば，簡単な数学的な処理で答えを得ることができます。

問8は，「$T$は惑星の運動の周期の$\frac{1}{4}$である」というミスが多発したように思われます。楕円軌道を描く惑星の運動周期の求め方としては，「ケプラーの第三法則を利用する」「楕円の面積を面積速度で割る」の2通りがありますが，後者の方法を利用すれば，本問のような中途半端な点に至るまでの時間も計算することができます。したがって，今回の問題では，下図の面積を面積速度で割る，という方法が正解です。

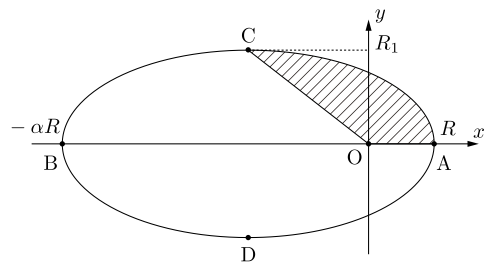
問9では，まずはじめに力学的エネルギーの和が$0$となっていることに気付き，その場合に惑星の軌道が放物線になることが分からないと何も始まりません。力学的エネルギーが$0$のときに無限遠方まで飛びされることは知っていると思うので，「惑星の軌道は楕円，放物線，双曲線のいずれか」という知識からなんとか放物線にたどり着きたいところです。問6で求めた$v_1$の式に$v_1=\sqrt{2}v_0$を代入すると，$\alpha\to\infty$が得られることからも推測が可能です。

最後の問10は放物線の数学的な解析になります。焦点と$x$切片の座標から放物線の式を求め，積分することで動径が掃く面積を計算する，という流れです。問8が解けていれば方針で戸惑うことはないと思われますが，時間内に数学的処理をしきれるかが問題でしょう。

第2問―直流回路，ダイオード

前半と後半で大きくテーマの変わる問題です。前半は直流回路の話で，計算処理がやや面倒であるものの，標準的な内容です。後半も共通問題は標準的な問題が多いですが，医学部問題は非常に難易度の高い交流の問題となっています。

問1から問3までは，直流回路の基本的な考え方で解き進めることができる内容です。各抵抗を流れる電流の値に注意しながら，キルヒホッフの第二法則でオーソドックスに解ける内容です。

問4は，訓練をしっかりと積んできた受験生に取ってはなんてことのない問題でしょう。相加相乗平均の関係を使う，という方針はすぐに見えるはずです。逆にこの方針が見えないと厳しい問題になります。

問5，問6はダイオードの特性曲線を利用して解く非オーム抵抗の内容です。ダイオードにかかる電圧，電流を真っ先に文字$V,\ I$で置く，という定石が身についていれば難なく解けるはずでしょう。非オーム問題の問題では，キルヒホッフの第二法則から得られる$V$と$I$の関係式を特性曲線に書き込む，という方針が一般的ですが，本問のように特性曲線が直線であり，数式化することが出来る場合には，キルヒホッフの第二法則と特性曲線の式を数式として連立して解く，という方針も取ることができる点は頭に入れておくべきです。

問7では，ダイオードの電流と電圧の積から消費電力を計算できることが理解できないと厳しいでしょう。この辺りで"分かっているかどうか"が問われます。回路のエネルギー保存の式が，キルヒホッフの第二法則と電流の積の積分から得られることが分かっているのであれば，あらゆる素子における消費電力が$VI$の形で表わされることは当然のこととして理解されます。とはいえこの話が分かっていなくとも，$VI$を計算すれば良さそう，という何となくの発想でも答えにたどり着けますし，電源の仕事と抵抗の消費電力から間接的に求めることも可能です。

問8，問9は平滑回路の問題です。問8はダイオードの働き（整流作用）が分かっていれば難なく解答できる問題です。2015年センター試験でも同様の出題が為されているので，失点は防ぎたい設問といえるでしょう。一方で，最後の問9は時間内に正しく状況を整理し，答えを導くことは非常に困難です。明らかに捨て問しょう。交流電圧を直流電圧に変換する「平滑回路」と呼ばれる回路についての問題ですが，知っている受験生はおそらくいないでしょうし，その場で考える高度な思考力が求められています。

平滑回路に関しては，こちらのページがとても参考になります。

来年に向けて

以上の問題分析からも分かる通り，2016年の物理の出題は，解ける問題は解ける，解けない問題は解けない，と，難易度の差がはっきりしていました。自分に解けるレベルの問題を適切に見極める物理の力，解ける問題を正確に計算し切る数学の力の双方を身につけるべく，日々訓練を行うのがよいでしょう。満点に近い点数で周囲に物理で差をつけようと思うと，高度な思考力と知識が必要となるので，相当高いレベルで物理を"理解"し，相当量の訓練を積む必要があります。これはあまり現実的とはいえないでしょう。